Řešení oběžné dráhy vymrštěného kyje, který má dopadnout zpět za rok

 

Kyj se bude pohybovat v meziplanetárním prostoru s gravitací ubývající podle vzdálenosti od Země.  Vytvoříme si matematický model, kde Zemi nahradíme hmotným bodem o hmotnosti původní zeměkoule a hypotetickým obalem či povrchem ideálně propustným pro prolétající kyje. Budeme řešit let kyje po eliptické dráze, mající v jednom ohnisku onen hmotný bod. Protože se má jednat o jakýsi svislý vrh, budeme hned od počátku uvažovat velkou výstřednost elipsy, aproximující onen vrh. Z celé elipsy  bude využita pouze nadzemní část, takže bude nutno určit, jak velká časová  chyba vznikne zanedbáním části trajektorie ležící pod virtuálním povrchem Země. Vliv ovzduší zanedbáváme. Závislost síly na vzdálenosti hmotného bodu od středu pohybu:

tj.

 

což je asi ta tvá původní  diferenciální rovnice.

Zrychlení při jakémkoliv pohybu hmotného bodu můžeme vyjádřit jako součet zrychlení axiálního a radiálního:

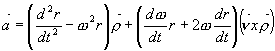
V našem případě středového pohybu je jednotkový vektor  kolmý na rovinu planetárního (kyjového) pohybu. Potom je zrychlení

tudíž

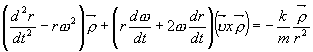
neboli

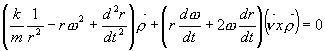
Tuto vektorovou diferenciální rovnici lze rozložit na 2 diferenciální rovnice skalární:

a druhá rovnice:

eliminací proměnné t (času):

kde C je dvojnásobek absolutní hodnoty plošné rychlosti

(už z toho čiší ten Kepler)

úpravou:

 dostaneme:

dosazením:

vynásobíme zlomkem  a upravíme:

což je již klasický tvar diferenciální rovnice typu

jejíž obecné řešení je:

použitím na předchozí výsledek:

z čehož plyne:

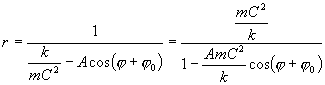
samozřejmě očekáváme kuželosečku, při použití polárních souřadnic bude:

a nebo:

 podle parametru epsilon dělíme kuželosečky na 3 typy:

   elipsa

   parabola

   hyperbola

 

Nás zajímá pouze první případ – vyhozený kyj se má vrátit

Porovnáním dostáváme:

, její parametr je

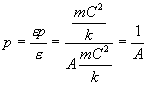
Integrační konstanty C, A,  vyplývají z počátečních podmínek.

C je dvojnásobek absolutní hodnoty konstantní plošné rychlosti,

Určení konstant A a

Když vektor rychlosti svírá s vektorem polohového vektoru úhel alfa,

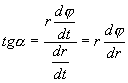
derivací dostaneme:

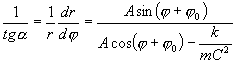
Zavedeme si počítání času od okamžiku, kdy  a současně

Další integrační konstanty už určíme z předchozích rovnic dosazením počátečních podmínek:

 

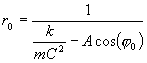
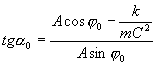
Pro elipsu s hlavní poloosou a a s excentricitou e je:

a vedlejší poloosa (ta nás ale nebude zajímat):

Doba oběhu je

 

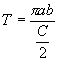
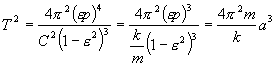
Při oběhu planety (kyje) okolo hmotného bodu na něj působí gravitační síla, že. Hmota kyje je m, hmota toho obletovaného bodu je M. Newtonova gravitační síla je

porovnáním s dostaneme

z toho už plyne

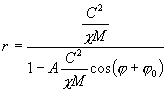
a oběžná doba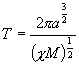

odstraníme nehezké exponenty

což je vyjádření Keplerových zákonů a také neklamné znamení, že jsme počítali dobře. Tento poznatek je pro nás zajímavý tím, že některé důležité parametry (pro nás oběžná doba) nejsou závislé na velikosti druhé (menší) poloosy. Dále že není důležitá hmotnost vymrštěného kyje, podstatná je pouze hmotnost Země. Teď už nám stačí např. získat údaje o jiné oběžnici Země bez ohledu na velikost druhé poloosy její trajektorie a přepočítat na náš případ. Touto testovací oběžnicí může být např. Měsíc, jehož parametry a parametry jeho oběžné dráhy jsou notoricky známé.

Výsledný vztah můžeme upravit na:

, kde u obsahuje všechny konstanty shodné v obou případech a které nepotřebujeme vyčíslit. V tomto tvaru je příslušný Keplerův zákon asi nejznámější.

Z něj plyne konstanta u platící pro tu kterou konkrétní planetu:

 

 

a pro jinou oběžnici této planety můžeme z doby oběhu vypočíst velikost její velké poloosy:

Parametry oběžné dráhy Měsíce: a=3,8.108m, T=2,36.106sec.

Dosazením vyjde u=10-13

Pro T=1rok=3,154.107 vteřin.

Dosazením do vzorce dostaneme a=2140014522m, z čehož plyne celková vzdálenost 2xa=4280029044m.

Nyní se zaměříme na bod trajektorie ležící 6000km od středu Země, tedy na jejím povrchu. V tomto bodě má kyj takovou rychlost, aby dolétl do uvedené vzdálenosti 4280029044m od středu Země. Z této rychlosti nás zajímá složka rovnoběžná s hlavní poloosou, určující dolet.

Určení potřebné rychlosti pro vržení kyje

Tíhové zrychlení ve vzdálenosti r od středu Země

Ze známé g=9,78ms-2 a r=6378245m nám vyjde

Na letící kyj tedy působí síla

Přeletem z bodu R do bodu B (po přímce procházející těžištěm Země) vykoná práci

Úbytek kinetické energie kyje musí být stejný:

 kde v0 je počáteční rychlost

V bodě obratu letu kyje, tj. největší vzdálenosti (apogeum), je v=0

pro kontrolu: úniková rychlost (neboli 2.kosmická rychlost):

Jejich  rozdíl činí cca 8.32m za sec, to bude teda pěkná fuška, aby o ten kyj nepřišel!

Zatím jsme mlčky předpokládali, že se doba letu kyje rovná celé oběžné době. Ve skutečnosti tomu tak není, těžiště Země je obíháno kolem dokola a otázka je, jak velká tím vznikne chyba, zda ji lze zanedbat či korigovat.

Zajímá nás, jaká je doba obletu kyje okolo těžiště Země pod jejím virtuálním povrchem našeho matematického modelu. Hned na první pohled je patrné, že kyj prolétající prakticky druhou kosmickou rychlostí zemský povrch směrem dolů a tím ještě rychlost zvyšující, se tam asi moc dlouho nezdrží.  Pro excentricitu platí

a pro perigeum, i když se vlastně v tomto případě nachází zatraceně hluboko pod zemí:

pro námi uvažovaný extrémní poměr a/b tuto funkci raději rozvedeme do řady, neboť by původní vztah již na počítači nemusel být stabilní.

Rozkladem do McLaurinovy řady (stačí jeden člen – ale ten druhý, první je nulový!)

Pro první přiblížení volíme b=1

což je vzdálenost úsměvně nepatrná, takže počítat rychlost v perigeu takovéto oběžné dráhy ztrácí smysl – určitě musí být nadrelativistická, pro nás však nemá fyzikální smysl, neboť kyj tuto dráhu absolvovat nebude. Důležité je, že otočka u takto pojaté dráhy je v šíleně mrňavém čase s exponentem velice záporným. Takže si jen hrubě vymezíme, jaký může být časový úsek trajektorie pro r<6000 km. Počáteční rychlost přesahuje 10 km/sec, celková dráha je 2xr= cca 12500km, čas tedy nemůže být delší, než 1250 sec, tj. cca 21 minut. To je v celkové oběžné dráze trvající 1 rok zanedbatelná část, nestojící za další námahu a ani v praxi by výpočet nebyl upřesňován, neboť je mnoho dalších vlivů způsobujících podstatně větší odchylky trajektorie. Z nich patrně největší bude vliv gravitace Měsíce a vliv slunečního větru. A vliv zemské atmosféry. Dále nelze opominout rychlost rotace Země při vyvržení kyje – v celém výpočtu byla uvažována nerotující Země. Tuto složku rychlosti lze buď využít nebo naopak musí být překonávána, záleží na okolnostech. Umělé družice ji využívají, jsou vždy vypouštěny tak, aby se rychlost rotace země přičítala k rychlosti nosné rakety. Proto obvykle na večerní obloze pozorujeme umělé družice letící od západu na východ, s různými sklony k rovníku.

 

Poznámka 1: Uvedená problematika zas není až tak moc bláznivá, například komety na oběžné dráze kolem Slunce mají velice výstředné (nikoliv výstřední) dráhy, takže v aféliu často vůbec nebývají pozorovatelné ani nejdokonalejšími dalekohledy, v perihéliu naopak často tvoří ozdobu noční oblohy pozorovatelnou prostým okem. Nutno uvážit, že jejich rozměr bývá třeba i jen několik kilometrů, takže jejich pozorovatelnost při odletu zaniká již při podstatně menších vzdálenostech, než je pozorovatelnost běžných planet. Např. nejpopulárnější Halleyova kometa známá už od starověku, nikdy nebyla pozorovatelná v odvrácené části dráhy. V současnosti se očekává, že s nejvyspělejší technikou to bude poprvé možné. Rušivé vlivy mají na komety někdy až fatální vliv, očekávaný přílet, tj. jejich přiblížení ke Slunci tak, aby byly pozorovatelné alespoň v dalekohledu, bývá pozměněn i o několik let vlivem událostí, které proběhly kdesi ve vesmíru v době, kdy nebyla pozorovatelná. Těmito vlivy bývá průlet okolo velkých planet, zejména Jupiter a Saturn. Parametry oběžné dráhy jsou samozřejmě stanovovány  jen podle pozorování v době, kdy ji je možno pozorovat. A tak komety překvapují astronomy nejen dobou příletu, ale i tvarem dráhy, neboť na rozdíl od hypotetického kyje prolétajícího okolo hypotetického středu Země kometa musí skutečně proletět v blízkosti Slunce a pokud ji pozměněná dráha přivede do přílišné blízkosti, potom se stává, že se tato krasavice obvykle složená z ledových balvanů a podobného materiálu, rozpadne. A tu se třeba náhle objeví jiná kometa, o které nikdo neměl ani tušení, neboť její oběžná doba činí několik set let a při posledních dvou, třech průletech bylo nad civilizovanými oblastmi nepříznivé počasí na pozorování či několik písmaznalých mudrců bylo právě prohlášeno za kacíře, odpadlíky, třídní nepřátele a ukřižováno, utopeno, upáleno či jinak utraceno pro pomluvu krále (faraona, velekněze, generálního tajemníka…nic nového pod Sluncem …) a jejich spisy naházeny do ohně. A my stejně jako naši předci před tisíciletími v úžasu zíráme na čarokrásné jevy na obloze, snažíme se je popsat, ale nemůžeme je nijak ovlivnit. Naštěstí. Alespoň zatím. Tečka.

 

 

Následné vztahy jsem chtěl použít pro exaktní odvození průletové doby pod hypotetickým povrchem, ale to už přenechám jiným záchvaťákům. Teď mám před sebou jiné odvozování ještě bláznivějších záležitostí, které budu prezentovat na mezinárodní konferenci podobně ujetých, to už je ale moc OT.

Plocha oběžné   dráhy kyje (je to elipsa)

Dvojnásobek plošné rychlosti tedy bude

Ta druhá poloosa je pro nás nezajímavá, symbolicky nastavená na b=1 a pro zeměkouli s vyvrženým kyjem dostaneme